Beyond Linear Scaling: How Software Systems Behave Under Load
Why adding more resources doesn't always increase throughput and how concurrency, contention, and coherency impact it.
I remember giving a presentation on serverless computing a few years ago, where I illustrated the concept of scalability as follows:
The figure shows linear scaling, a line growing and shooting infinitely to the top. For each added load unit, you get an equal gain in throughput (e.g., the number of users or data records the system can handle). There are certain (and very specific) situations where scalability works like that; for example, independently parallelizable tasks like text search, where each subtask looks for keywords in separate parts of the entire text. The result is then a matter of combining outputs from the previously executed subtasks.
However, this is different from how scalability works in general. As soon as you look at entire, complex systems instead of individual, parallelizable algorithms, the issue gets more complicated…
Concurrency
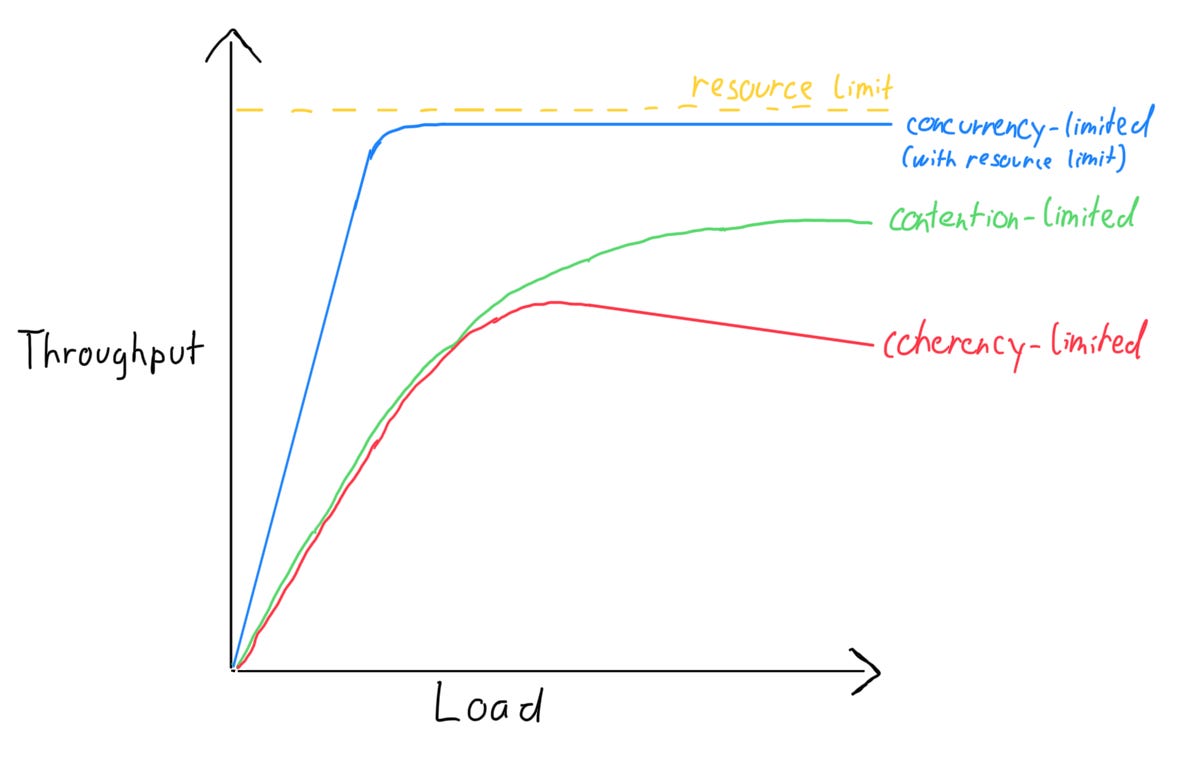
The first issue such a system often encounters is hitting a resource limit — for example, when subtasks share a resource pool and reach its capacity. Initially, the throughput increases approximately linearly, but as it approaches the resource limit, the gain in throughput gradually diminishes and fades out.
In these cases, the system’s throughput is limited by its concurrency and may hit an upper bound once it exhausts the available resource pool.
Shared Resources
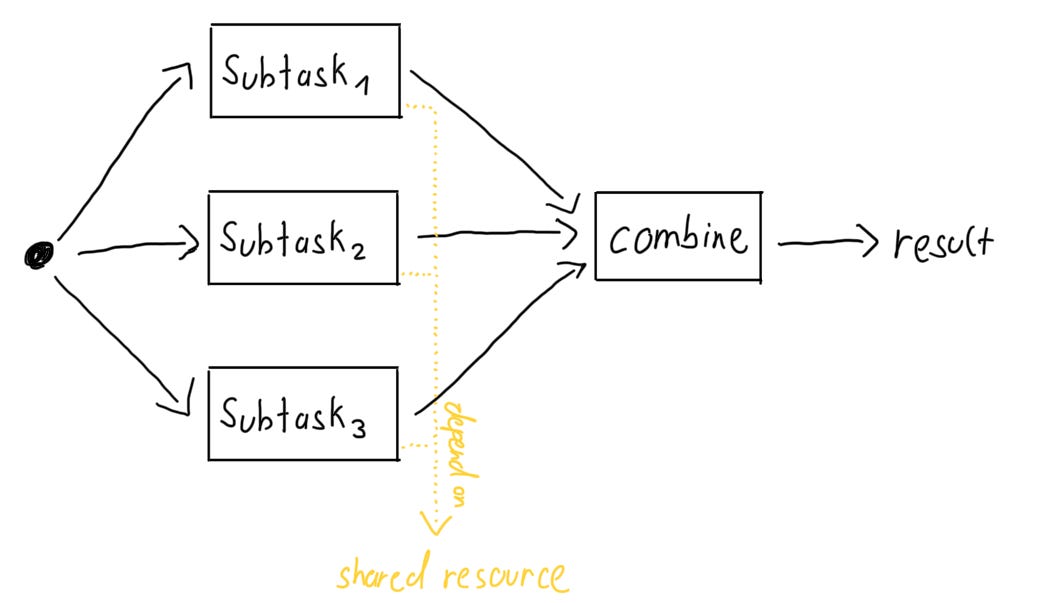
Subsystems competing for resources may also inhibit throughput gain. Let's look at the following system:
Although the subtasks can run concurrently, they depend on a shared resource. This shared resource could be computational (e.g., CPU), network-related (e.g., bandwidth), or infrastructure (e.g., a lock on a common table). If one subtask exhausts the shared resource, the other subtasks slow down significantly or may even need to stop and wait until enough resources become available again.
This slows down scalability and disrupts the linear increase in throughput compared to the example before. As resources become increasingly saturated, subtasks effectively interfere with each other, and the gain in throughput per additional load unit slows down.
In this scenario, the system's throughput is limited by its subparts contention over shared resources. As you can see, the gain of throughput per additional load unit slows considerably.
Maintaining Consistency
In certain systems, adding more load can actually decrease throughput. Let's examine the following system:
The three subtasks each have their own data storage, either persistently through separate data stores or ephemerally via caches. Let's assume the system must maintain consistency to respond correctly. Imagine one subtask updating data in its own storage; the system must then propagate these changes to other storages using a transaction.
This has significant consequences. Not only do the subtasks need to stop responding until a consistent state is restored, but the process of re-establishing this state requires additional work before the system can resume service. This overhead negatively affects throughput: as more load is added, the throughput actually decreases—a phenomenon often observed in real-world throughput metrics.
Thus, the throughput of the system is limited by the amount of coherency it needs to maintain.
The Universal Scalability Law
The dynamics I laid out above are described in a model called the Universal Scalability Law, formulated by researcher Neil Gunther back in 1993:
C(N) represents the relative throughput given a load of N. It is relative in the sense that X(N) defines the absolute throughput, and C(N) = X(N) / X(1).
Gunther refers to the scalability effects from above as "The Three Cs":
Concurrency-limited scalability is proportionally linear because α = 0 and β = 0 (see Figure 1). You should expect a scaling limit, as shown in Figure 3, but the equation above does not explicitly contain one. (Note: To illustrate effects such as reaching a resource limit more intuitively, the illustrations above use the absolute throughput (X(N)) on their vertical axis instead of the relative throughput (C(N)) discussed in this section. Gunther also provides a generalized form of the equation for X(N).)
Contention-limited scalability is the effect of slowing down throughput gains, as shown in Figure 5. It occurs when α > 0 and β still equals 0.
Coherency-limited scalability is the negative throughput gain due to extra work to keep the system consistent, as shown in Figure 7. It is the case when α and β are both greater than 0.
How to Use the Universal Scalability Law
Suppose you have made a few measurements by subjecting the system under a particular load and measuring its throughput. You can use the equation above to extrapolate further data points. This helps you assess load scenarios that you have not measured yet or are not able to measure. Gunther states that you need at least around six data points to do this.
You could also take measurements, fit a curve from the above equation, and estimate values for contention (α) and coherency (β). These estimates, alongside the system's throughput, could serve as holistic fitness functions evaluating the scalability properties of your system. In "Architectural Fitness Functions: Building Effective Feedback Mechanisms for Quality Attributes", I have written about holistic fitness functions:
We need effective and (if possible) automated [feedback] mechanisms, especially for quality attributes. The book "Building Evolutionary Architectures: Automated Software Governance" introduced a term for feedback mechanisms on quality attributes borrowed from evolutionary algorithms: (architectural) fitness functions.
In short, an (architectural) fitness function evaluates the system with regard to a quality attribute. You can distinguish fitness functions by the scope of their evaluation:
[…]
Fitness functions can also be holistic. They test the entire system or large parts of it and assess specific quality attributes. For example, they might measure response times or observe the system after being put under load. Holistic fitness functions are usually more complex and expensive to build.
Conclusion
The Universal Scalability Law not only provides deeper intuitions into how scalability works but also aids in analyzing a system’s behavior under load. It serves as both a mental model and a practical tool for evaluating a system’s scalability. You can use the insights generated by the model to discover and prioritize improvements to reduce contention and coherency overhead as needed.
Further Reading and References
If you want to understand the Universal Scalability Law in more detail and discover further usage scenarios and tools, I recommend this article by Neil Gunther.
For a more elaborated discussion on scalability models and how to obtain the graphs from above, see “Getting in the Zone for Successful Scalability”.